- Home
- Machinery Directive
- History of the Machinery Directive 2006/42/EC
- Machinery directive 2006/42/EC
- Whereas of machinery directive 2006/42/EC
- Articles of machinery directive 2006/42/EC
- Article 1 of machinery directive 2006/42/EC - Scope
- Article 2 of machinery directive 2006/42/EC - Definitions
- Article 3 : Specific Directives of machinery directive 2006/42/EC
- Article 4 : Market surveillance of machinery directive 2006/42/EC
- Article 5 : Placing on the market and putting into service - machinery directive 2006/42/EC
- Article 6 : Freedom of movement - machinery directive 2006/42/EC
- Article 7 : Presumption of conformity and harmonised standards - machinery directive 2006/42/EC
- Article 8 : Specific measures - machinery directive 2006/42/EC
- Article 9 : Specific measures to deal with potentially hazardous machinery - machinery directive 2006/42/EC
- Article 10 : Procedure for disputing a harmonised standard - machinery directive 2006/42/EC
- Article 11 : Safeguard clause - machinery directive 2006/42/EC
- Article 12 : Procedures for assessing the conformity of machinery - machinery directive 2006/42/EC
- Article 13 : Procedure for partly completed machinery - 2006/42/EC
- Article 14 : Notified bodies - machinery directive 2006/42/EC
- Article 15 : Installation and use of machinery - machinery directive 2006/42/EC
- Article 16 : CE marking - machinery directive 2006/42/EC
- Article 17 : Non-conformity of marking - machinery directive 2006/42/EC
- Article 18 : Confidentiality - machinery directive 2006/42/EC
- Article 19 : Cooperation between Member States - machinery directive 2006/42/EC
- Article 20 : Legal remedies - machinery directive 2006/42/EC
- Article 21 : Dissemination of information - machinery directive 2006/42/EC
- Article 22 : Committee - machinery directive 2006/42/EC
- Article 23 : Penalties - machinery directive 2006/42/EC
- Article 24 : Amendment of Directive 95/16/EC - machinery directive 2006/42/EC
- Article 25 : Repeal - machinery directive 2006/42/EC
- Article 26 : Transposition - machinery directive 2006/42/EC
- Article 27 : Derogation - machinery directive 2006/42/EC
- Article 28 : Entry into force - machinery directive 2006/42/EC
- Article 29 : Addressees - machinery directive 2006/42/EC
- ANNEX I of machinery directive 2006/42/EC - Summary
- GENERAL PRINCIPLES of annex 1 of machinery directive 2006/42/EC
- 1 ESSENTIAL HEALTH AND SAFETY REQUIREMENTS of annex 1 - definitions - machinery directive 2006/42/EC
- Article 1.1.2. Principles of safety integration of annex 1 machinery directive 2006/42/EC
- Article 1.1.3. Materials and products annex 1 machinery directive 2006/42/EC
- Article 1.1.4. Lighting - annex 1 machinery directive 2006/42/EC
- Article 1.1.5. Design of machinery to facilitate its handling - annex 1 machinery directive 2006/42/EC
- Article 1.1.6. Ergonomics - annex 1 machinery directive 2006/42/EC
- Article 1.1.7. Operating positions - annex 1 machinery directive 2006/42/EC
- Article 1.1.8. Seating - annex 1 machinery directive 2006/42/EC
- Article 1.2.1. Safety and reliability of control systems - annex 1 of machinery directive 2006/42/EC
- Article 1.2.2. Control devices - annex 1 of machinery directive 2006/42/EC
- Article 1.2.3. Starting - annex 1 of machinery directive 2006/42/EC
- Article 1.2.4. Stopping - annex 1 of machinery directive 2006/42/EC
- Article 1.2.4.4. Assembly of machinery - Annex 1 of machinery directive 2006/42/EC
- Article 1.2.5. Selection of control or operating modes - annex 1 of machinery directive 2006/42/EC
- Article 1.2.6. Failure of the power supply - annex 1 of machinery directive 2006/42/EC
- Article 1.3. PROTECTION AGAINST MECHANICAL HAZARDS - annex 1 of machinery directive 2006/42/EC
- Article 1.4. REQUIRED CHARACTERISTICS OF GUARDS AND PROTECTIVE DEVICES - annex 1 of machinery directive 2006/42/EC
- Article 1.5. RISKS DUE TO OTHER HAZARDS - annex 1 of machinery directive 2006/42/EC
- Article 1.6. MAINTENANCE - annex 1 of machinery directive 2006/42/EC
- Article 1.7. INFORMATION - annex 1 of machinery directive 2006/42/EC
- Article 2. SUPPLEMENTARY ESSENTIAL HEALTH AND SAFETY REQUIREMENTS - annex 1 machinery directive 2006/42/EC
- Article 3. SUPPLEMENTARY ESSENTIAL HEALTH TO THE MOBILITY OF MACHINERY - annex 1 machinery directive 2006/42/EC
- Article 4. SUPPLEMENTARY REQUIREMENTS TO OFFSET HAZARDS DUE TO LIFTING OPERATIONS of machinery directive 2006/42/EC
- Article 5. SUPPLEMENTARY ESSENTIAL HEALTH AND SAFETY REQUIREMENTS FOR UNDERGROUND WORK of machinery directive 2006/42/EC
- Article 6. SUPPLEMENTARY REQUIREMENTS - HAZARDS DUE TO THE LIFTING OF PERSONS of machinery directive 2006/42/EC
- Annex II : Declarations of CONFORMITY OF THE MACHINERY, DECLARATION OF INCORPORATION - machinery directive 2006/42/EC
- Annex III of machinery directive 2006/42/EC - CE marking
- Annex IV of machinery directive 2006/42/EC
- Annex V of machinery directive 2006/42/EC
- Annex VI of machinery directive 2006/42/EC
- Annex VII - Technical file for machinery - machinery directive 2006/42/EC
- Annex VIII - Assessment of conformity of machinery directive 2006/42/EC
- Annex IX of machinery directive 2006/42/EC - EC type-examination
- Annex X of machinery directive 2006/42/EC - Full quality assurance
- Annex XI of machinery directive 2006/42/EC - Minimum criteria for the notification of bodies
- Annex XII of machinery directive 2006/42/EC - Correlation table between machinery directive 2006/42/CE and MD 1998/37/CE
- Machinery directive 1998/37/EC
- considerings of machinery directive 1998/37/CE
- articles of 1998/37/EC machinery directive
- Annex I of 1998/37/CE machinery directive
- Annex II of 1998/37/EC machinery directive
- Annex III of machinery directive 1998/37/CE
- Annex IV of machine directive 1998/37/EC
- Annex V of machines directive 1998/37/CE
- Annex VI of machines directive 1998/37/EC
- Annex VII of machines directive 1998/37/EC
- Annex VIII of 1998/37/CE machine directive
- Annex IX of machinery directive 1998/37/CE
- Machinery directive 1989/392/EC
- whereas of machinery directive machines 1989/392/EEC
- articles of machinery directive 1989/392/EEC
- Annex I of machinery directive 1989/392/EEC
- Annex II of machine directive 1989/392/EEC
- Annex III of machinery directive 1989/392/EEC
- Annex IV of machinery directive 1989/392/EEC
- Annex V of machinery directive 1989/392/EEC
- Annex VI of machine directive 1989/392/EEC
- Annexe VII of machinery directive 1989/392/EEC
- Amendments of 1989/392/EEC directive
- ATEX directives
- ATEX 94/9/EC directive
- Whereas of ATEX 94/9/CE directive
- Articles of ATEX 94/9/CE directive
- article 1 ATEX 94/9/EC directive
- article 2 ATEX 94/9/EC directive
- article 3 ATEX 94/9/EC directive
- article 4 : ATEX 94/9/EC directive
- article 5 : ATEX 94/9/EC directive
- article 6 : ATEX 94/9/EC directive
- article 7 : ATEX 94/9/EC directive
- article 8 ATEX 94/9/EC directive
- article 9 : ATEX 94/9/EC directive
- article 10 : ATEX 94/9/EC directive
- article 11 : ATEX 94/9/EC directive
- article 12 : ATEX 94/9/EC directive
- article 13 : ATEX 94/9/EC directive
- article 14 : ATEX 94/9/EC directive
- article 15 : ATEX 94/9/EC directive
- article 16 : ATEX 94/9/EC directive
- ANNEX I of ATEX 94/9/EC directive : CRITERIA DETERMINING THE CLASSIFICATION OF EQUIPMENT-GROUPS INTO CATEGORIES
- ANNEX II of ATEX 94/9/EC : directive ESSENTIAL HEALTH AND SAFETY REQUIREMENTS -EHSR
- ANNEX III of ATEX 94/9/EC directive : MODULE EC-TYPE EXAMINATION
- ANNEX IV of ATEX 94/9/EC directive : MODULE PRODUCTION QUALITY ASSURANCE
- ANNEX V of ATEX 94/9/EC directive : MODULE PRODUCT VERIFICATION
- ANNEX VI of ATEX 94/9/EC directive : MODULE CONFORMITY TO TYPE
- ANNEX VII of ATEX 94/9/EC directive : MODULE PRODUCT QUALITY ASSURANCE
- ANNEX VIII of ATEX 94/9/EC directive : MODULE INTERNAL CONTROL OF PRODUCTION
- ANNEX IX of ATEX 94/9/EC directive : MODULE UNIT VERIFICATION
- ANNEX X of ATEX 94/9/EC directive : CE Marking - Content of the EC declaration of conformity
- ANNEX XI of ATEX 94/9/EC directive: NOTIFICATION OF BODIES
- ATEX 99/92/EC Directive
- ATEX DIRECTIVE 2014/34/UE
- whereas of 2014/34/UE ATEX directive
- Articles of ATEX 2014/34/UE directive
- Annex 1 of ATEX 2014/34/UE directive
- Annex 2 of the ATEX 2014/34/UE directive
- Annex 3 of ATEX 2014/34/UE directive
- Annex 4 of ATEX 2014/34/UE directive
- Annex 5 of ATEX 2014/34/UE directive
- Annex 6 of ATEX 2014/34/UE directive
- Annex 7 of ATEX 94/9/EC directive
- Annex 8 of the ATEX 2014/34/UE directive
- Annex 9 of the ATEX 2014/34/UE directive
- Annex 10 of ATEX 2014/34/UE directive
- Annex 11 of ATEX 2014/34/UE directive
- Annex 12 of the ATEX 2014/34/UE directive
- Audits in Ex field - EN 13980, OD 005 and EN ISO/CEI 80079-34
- New ATEX directive
- RASE european project
- ATEX 94/9/EC directive
- IECEX
- Standardization & European Regulation
- Safety of machines : Standardization and European regulations
- European regulation for machines - standardization for machines - harmonized standards
- Standardization in machinery
- EN ISO 12100 - Décembre 2010
- EN ISO 12100-1 - January 2004
- EN ISO 12100-1:2003/A1
- EN ISO 12100-2 November 2003
- EN ISO 12100-2:2003/A1
- EN ISO 14121-1 September 2007
- ISO/TR 14121-2 - 2007
- EN 50205:2002 standard - Relays with forcibly guided (mechanically linked) contacts
- ISO 11161:2007
- ISO 13849-1:2006
- ISO 13849-2:2012
- ISO 13850:2006 - Safety of machinery -- Emergency stop -- Principles for design
- ISO 13851:2002 - Safety of machinery -- Two-hand control devices -- Functional aspects and design principles
- ISO 13854:1996 Safety of machinery - Minimum gaps to avoid crushing of parts of the human body
- ISO 13855:2010 - Safety of machinery -- Positioning of safeguards with respect to the approach speeds of parts of the human body
- ISO 13856-1:2013 Safety of machinery -- Pressure-sensitive protective devices -- Part 1: General principles
- ISO 13856-2:2013 - Safety of machinery -- Pressure-sensitive protective devices -- Part 2: General principles for design testing
- ISO 13856-3:2013 Safety of machinery -- Pressure-sensitive protective devices - Part 3: General principles for design
- ISO 13857:2008 Safety of machinery -- Safety distances to prevent hazard zones
- ISO 14118:2000 - Safety of machinery -- Prevention of unexpected start-up
- ISO 14119:2013- Interlocking devices associated with guards
- ISO 14120:2002 - Guards -- General requirements for the design and construction
- ISO 14122-1:2001 - Permanent means of access to machinery
- ISO 14122-2:2001 - Permanent means of access to machinery
- ISO 14122-4:2004 - Permanent means of access to machinery
- ISO 14123-1:1998 - Reduction of risks to health from hazardous substances emitted by machinery
- ISO 14123-2:1998 - Reduction of risks to health from hazardous substances emitted by machinery
- ISO 14159:2002 - Hygiene requirements for the design of machinery
- ISO 19353:2005 -- Fire prevention and protection
- ISO/AWI 17305 - Safety of machinery - Safety functions of control systems
- ISO/DTR 22100-2 - Safety of machinery -- Part 2: How ISO 12100 relates to ISO 13849-1
- ISO/TR 14121-2:2012 - Risk assessment - Part 2: Practical guidance
- ISO/TR 18569:2004 - Guidelines for the understanding and use of safety of machinery standards
- ISO/TR 23849:2010 - Guidance on the application of ISO 13849-1 and IEC 62061 in the design of safety-related control systems
- STABILITY DATES FOR Machinery STANDARDS
- harmonized standards list - machinery-directive 2006/42/CE
- Publication of harmonised standards for machinery directive 2006/42/EC - 9.3.2018
- Harmonized standard list - machinery directive 2006/42/EC - 9.6.2017
- Harmonized standards for machinery - OJ C 2016/C173/01 of 15/05/2016
- Harmonized standards for machinery -OJ C 2016/C14/102 of 15/01/2016
- Harmonized standards for machinery - corrigendum OJ C 2015/C 087/03 of 13/03/2015
- harmonized standards for machinery - OJ C 2015/C 054/01 of 13/02/2015
- Application guide for machinery directive 2006/42/EC
- Guide to application of the machinery directive 2006/42/CE - July 2017
- Guide to application of the Machinery Directive 2006/42/EC - second edition June 2010
- Guide to application of machinery directive - 1-2 : The citations
- Guide to application of machinery directive - § 3 to § 31 The Recitals
- Guide to application of machinery directive - § 32 to § 156 - The Articles
- Guide to application of machinery directive - § 157 to § 381 - Annex I
- Guide to application of machinery directive - § 382 to § 386 - ANNEX II Declarations
- Guide to application of machinery directive - § 387 - ANNEX III CE marking
- recommendation for use - machinery directive 2006/42/EC
- Notified bodies under the machinery directive 2006/42/CE
- Safety of Ex, ATEX and IECEx equipments : Standardization
- Standardization in Ex Field
- The transposition of the ATEX 94/9/EC Directive to the 2014/34/EU directive
- harmonized standards list - ATEX directive 2014/34/EU
- Harmonized standard list for ATEX 2014/34/UE - 12-10-2018
- Harmonized standard list for ATEX 2014/34/UE - 15.6.2018
- Harmonized standard list for ATEX 2014/34/UE - 12-07-2019
- Harmonized standard list for ATEX 2014/34/UE - 9.6.2017
- Harmonized standards list ATEX 2014/34/UE directive - OJ C 126 - 08/04/2016
- Guide to application of the ATEX Directive 2014/34/EU
- application guide of 2014/34/EU directive - preambule, citations and recitals
- Guide to application of the ATEX 2014/34/UE directive - THE ARTICLES OF THE ATEX DIRECTIVE
- Guide to application of the ATEX 2014/34/UE directive - ANNEX I CLASSIFICATION INTO CATEGORIES
- Guide to application of the ATEX 2014/34/UE directive - ANNEX II ESSENTIAL HEALTH AND SAFETY REQUIREMENTS
- Guide to application of the ATEX 2014/34/UE directive - ANNEX III MODULE B: EU-TYPE EXAMINATION
- Guide to application of the ATEX 2014/34/UE directive - ANNEX IV MODULE D: CONFORMITY TO TYPE
- Guide to application of machinery directive - § 388 - ANNEX IV machinery and mandatory certification
- Guide to application of the ATEX 2014/34/UE directive - ANNEX V MODULE F: CONFORMITY TO TYPE
- Alignment of ten technical harmonisation directives - Decision No 768/2008/EC
- ATEX 94/9/EC directive documents
- ATEX 94/9/EC guidelines
- ATEX 94/9/EC guidelines 4th edition
- 1 INTRODUCTION of ATEX 94/9/EC guidelines 4th edition
- 2 OBJECTIVE OF THE ATEX DIRECTIVE 94/9/EC - ATEX 94/9/EC guidelines 4th edition
- 3 GENERAL CONCEPTS of ATEX 94/9/EC directive ATEX 94/9/EC guidelines 4th edition
- 4 IN WHICH CASES DOES DIRECTIVE 94/9/EC APPLY - ATEX 94/9/EC guidelines 4th edition
- 5 EQUIPMENT NOT IN THE SCOPE OF DIRECTIVE 94/9/EC - ATEX 94/9/EC guidelines 4th edition
- 6 APPLICATION OF DIRECTIVE 94/9/EC ALONGSIDE OTHERS THAT MAY APPLY - ATEX 94/9/EC guidelines 4th edition
- 7 USED, REPAIRED OR MODIFIED PRODUCTS AND SPARE PARTS - ATEX 94/9/EC guidelines 4th edition
- 8 CONFORMITY ASSESSMENT PROCEDURES - ATEX 94/9/EC guidelines 4th edition
- 9 NOTIFIED BODIES - ATEX 94/9/EC guidelines 4th edition
- 10 DOCUMENTS OF CONFORMITY - ATEX 94/9/EC guidelines 4th edition
- 11 MARKING - CE marking -ATEX 94/9/EC guidelines 4th edition
- 12 SAFEGUARD CLAUSE AND PROCEDURE - ATEX 94/9/EC guidelines 4th edition
- 13 EUROPEAN HARMONISED STANDARDS - ATEX 94/9/EC guidelines 4th edition
- 14 USEFUL WEBSITES - ATEX 94/9/EC guidelines 4th edition
- ANNEX I: SPECIFIC MARKING OF EXPLOSION PROTECTION - ATEX 94/9/EC guidelines 4th edition
- ANNEX II: BORDERLINE LIST - ATEX PRODUCTS - ATEX 94/9/EC guidelines 4th edition
- ATEX 94/9/EC guidelines 4th edition
- Harmonized standards list - ATEX 94/9/EC directive
- Harmonized standards list ATEX 94/9/EC directive - OJ C 126 - 08/04/2016
- Harmonized standards list ATEX 94/9/EC - OJ C 335 - 09/10/2015
- Harmonized standards list ATEX 94/9/EC - OJ-C 445-02 - 12/12/2014
- Harmonized standards list ATEX 94/9/EC - OJ-C 076-14/03/2014
- Harmonized standards list ATEX 94/9/EC - OJ-C 319 05/11/2013
- ATEX 94/9/EC guidelines
- European regulation for ATEX 94/9/EC ATEX directive
- Guide to application of ATEX 2014/34/EU directive second edition
- Safety of machines : Standardization and European regulations
- Latest news & Newsletters
- Functional safety
- Terms and definitions for functional safety
- Safety devices in ATEX
- The SAFEC project
- main report of the SAFEC project
- Appendix 1 of the SAFEC project - guidelines for functional safety
- Appendix 2 of the SAFEC project
- ANNEX A - SAFEC project - DERIVATION OF TARGET FAILURE MEASURES
- ANNEX B - SAFEC project - ASSESSMENT OF CURRENT CONTROL SYSTEM STANDARDS
- ANNEX C - safec project - IDENTIFICATION OF “USED SAFETY DEVICES”
- Annex D - SAFEC project - study of ‘ Used Safety Devices’
- Annex E - Determination of a methodology for testing, validation and certification
- EN 50495 standard for safety devices
- The SAFEC project
- Safety components in Machinery
- STSARCES - Standards for Safety Related Complex Electronic Systems
- STSARCES project - final report
- STSARCES - Annex 1 : Software engineering tasks - Case tools
- STSARCES - Annex 2 : tools for Software - fault avoidance
- STSARCES - Annex 3 : Guide to evaluating software quality and safety requirements
- STSARCES - Annex 4 : Guide for the construction of software tests
- STSARCES - Annex 5 : Common mode faults in safety systems
- STSARCES - Annex 6 : Quantitative Analysis of Complex Electronic Systems using Fault Tree Analysis and Markov Modelling
- STSARCES - Annex 7 : Methods for fault detection
- STSARCES - Annex 8 : Safety Validation of Complex Components - Validation by Analysis
- STSARCES - Annex 9 : safety Validation of complex component
- STSARCES - Annex 10 : Safety Validation of Complex Components - Validation Tests
- STSARCES - Annex 11 : Applicability of IEC 61508 - EN 954
- STSARCES - Annex 12 : Task 2 : Machine Validation Exercise
- STSARCES - Annex 13 : Task 3 : Design Process Analysis
- STSARCES - Annex 14 : ASIC development and validation in safety components
- Functional safety in machinery - EN 13849-1 - Safety-related parts of control systems
- STSARCES - Standards for Safety Related Complex Electronic Systems
- History of standards for functional safety in machinery
- Basic safety principles - Well-tried safety principles - well tried components
- Functional safety - detection error codes - CRC and Hamming codes
- Functional safety - error codes detection - parity and chechsum
- Functional safety and safety fieldbus
- ISO 13849-1 and SISTEMA
- Prevention of unexpected start-up and machinery directive
- Self tests for micro-controllers
- Validation by analysis of complex safety systems
- basic safety principles - safety relays for machinery
- Download center
- New machinery regulation
- Revision of machinery directive 2006/42/EC
- security for machines
Functional safety - detection error codes - CRC and Hamming codes
1 CRC (Cyclic Redundancy Check)
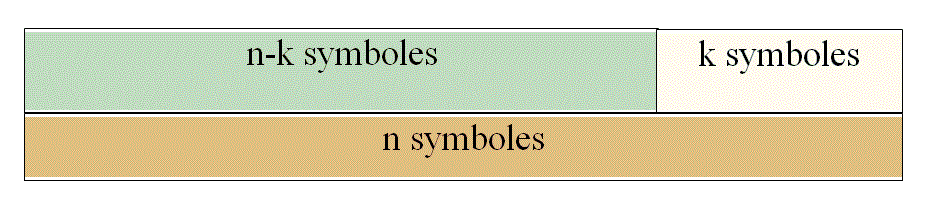
The CRC is an encoding method that consist to group when transmitting information in words of "n-k" bits and to associate them to a word of "n" bits. The redundancy consists of the "k" bits. The number of possible words of "n" elements is "2 n-k" and the other words correspond to words affected by errors.
The methods of "verification by key" objectives are to compress the information. From a finished sequence of information of length "n-k" , a compression mechanism (CRC - Cyclic Redundancy Check), characterizes this sequence of information with condensed information: the key. This key does not correct the errors, this key can detect the differences between several sequences.
 |
1.1.Error detection Mecanism
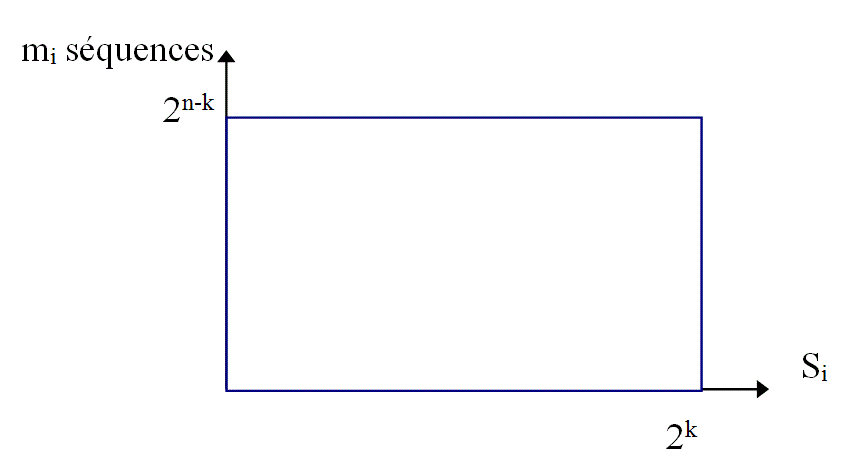
Consider the following data:
- m i = the number of sequences of informationhaving the same key .
- n-k = size of the information sequence (fixed or variable).
- k = key size (resulting from the polynomial division).
- n = size of the message.
The verification mechanism with key is to compress a message consisting of "n-k" symbols in a finite number of bits (k) .
Each key, of resulting value"S i" is representative of a number "m i" of sequences of information of fixed or variable size. The key "S i", is a word of 'k' bits that can take "2k" different values.
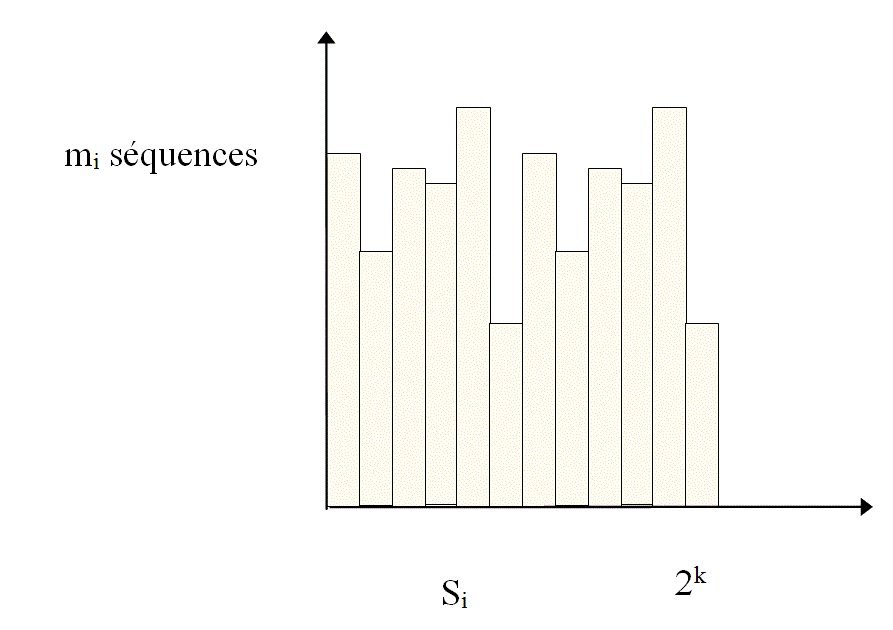 |
For an information sequence "mi" of constant size "n" , there are 2n possible forms, and each of these form, there is only one possible key whose value is comprised between "0" and "2k " and the following is obtained:
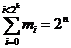
The probability of detection of error for a sequence "m i" (rpresented by the key "Si") represent the probability of obtain the same value of the key "S i" from an erroneous sequence "m i" .
The probability of detection of error associated with a key "S i", 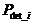 is defined as follows:
is defined as follows:
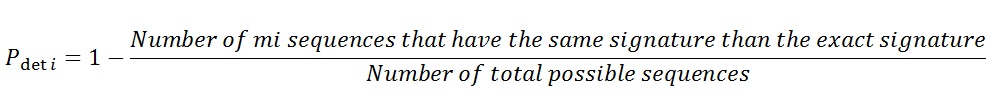
mi-1 : represents the number of m-sequences mi having the same key as the exact sequence,
2n-1 : correspond to the total number of possible sequences (2n) minus the exact sequence (1).
Either:
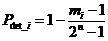
In order to calculate the average detection power, we must sum all the cases corresponding to "mi" information sequences. There are m i sequences of information whose probability of error detection is P det_i. The average value for all the "2n" possible sequences is :
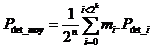
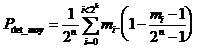
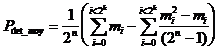
or
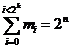 ,
,
from where
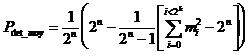
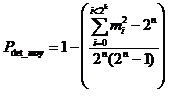
In the case of networks transmission, "n" is not generally constant (frames vary in length). Therefore, the residual errors are composed of all the possible combinations of errors on different frame length.
An "m i" sequence information can be written as follows:
mi = « 2n-k + xi »,
Thus we get:
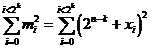
whether
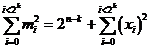
Are derived from the above formula that the probability of error detection of a compression mechanism is maximum when m i is constant regardless Si,
we obtain mi = 2n-k :
And we have:
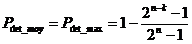
When the key is a constant number of information sequences, the probability of error detection is optimal.
Otherwise, if there is a different number of information sequences, the probability of error detection will be less than Pdet max and must be estimated in each case.
1.2.Properties and choice of a polynomial generator key
The polynomials generator keys are generally classified into the following three types, regardless of their degree:
· Irreducible polynomials
- A polynomial of degree k is irreducible if it is not divisible by a polynomial of degree less than k, except by 1.
For instance,
a(x) = x4  x3
x3  x2
x2  x
x  1 of degree 4, and
1 of degree 4, and
b(x) = x8  x4
x4  x3
x3  x 1 of degree 8,
x 1 of degree 8,
are irreducible polynomials.
primitive polynomials
- An irreducible polynomial of degree k is primitive if it is a divisor of the polynomial xn - 1 with n = 2k - 1, without the fact to be a divisor of all polynomial of xm - 1 where m < n. This polynomial may also be divisor of certain polynomials xp - 1 where p> n.
Irreducible or primitive polynomials are obtained by a complex mathematical algorithm that is difficul to perform manually if the level is high. Note that there are still primitive polynomials whatever the desired degree.
· The arbitrary polynomial (nor irreducible nor primitive)
Detect the maximum possible error generator polynomial key aims. For that he must comply with the following rules:
1 - if we take a key s(x) corresponding to the input sequence m(x) and obtained using the generator polynomial g(x) primitive and irreducible. If we call e(x) an error sequence, ie which has "1" in the wrong locations and "0" elsewhere, then the origin message m(x) and the wrong message m(x)  e(x) have the same key s(x) if and only if e(x) is a multiple of g(x) modulo 2.
e(x) have the same key s(x) if and only if e(x) is a multiple of g(x) modulo 2.
Therefore, the smaller erroneous sequence is g(x), where:
2 - If the generator polynome is of degree k, any errors that may affect an input sequence of length n £ k are detected. It is then possible to determine the number of undetected erroneous ³ for n k sequences, as they are all multiples of g (x).
The length input sequences correspond to n polynomials of degree n-1. There is thus 2 n -1 possible sequences for each polynomial has "n" and these coefficients may take "0" or "1" values.
We prove by induction that there are N = 2 nk - 1 erroneous sequences that are undetectable. Thus, for m = n, we obtain 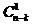 erroneous base sequences,
erroneous base sequences, 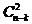 erroneous sequences by combining base pairs, etc ..., and finally an erroneous sequences by combining all base sequence sequences or
erroneous sequences by combining base pairs, etc ..., and finally an erroneous sequences by combining all base sequence sequences or 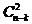 . From where:
. From where:
2 - Si le polynôme générateur est de degré k, toutes les erreurs pouvant affecter une séquence d’entrées de longueur n £ k sont détectées. Il est alors possible de déterminer le nombre de séquences erronées non détectées pour n ³ k, car elles sont toutes multiples de g(x).
Les séquences d’entrée de longueur n correspondent à des polynômes de degré n-1. Il y a donc 2n-1 séquences possibles car chaque polynôme a « n » coefficients et ceux-ci peuvent prendre les valeurs « 0 » ou « 1 ».
On démontre par récurrence qu’il y a N = 2n-k - 1 séquences erronées qui sont indétectables. Ainsi, pour m = n, on obtient 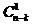 séquences erronées de base,
séquences erronées de base, 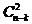 séquences erronées en combinant les séquences de base deux à deux, etc..., et enfin une séquence erronée en combinant toutes les séquences de base, soit
séquences erronées en combinant les séquences de base deux à deux, etc..., et enfin une séquence erronée en combinant toutes les séquences de base, soit 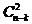 . D’où :
. D’où :
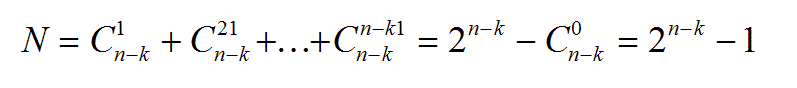
3 - Pour une séquence d’entrées de longueur « n » avec « n-k », la probabilité pour que le générateur de clé de degré k ne détecte pas d’erreurs, est égale à [2n-k-1]/[2n-1]. Ceci en supposant que toutes les séquences erronées ont une probabilité d’apparition identique. Lorsque n est très grand, le rapport tend vers 2-k. Cette propriété est la plus importante car elle caractérise avec précision le pouvoir de détection P de l’analyse de clé qui est presque uniquement fonction du degré du polynôme générateur choisi.
4 - Tout générateur de clé construit à partir d’un polynôme générateur qui possède au moins deux coefficients non nuls, détecte toutes les erreurs simples.
5 - Tout générateur de clé construit à partir d’un polynôme générateur contenant (xhÅ1) en facteur, détecte toutes les erreurs impaires.
6 - Tout générateur de clé construit à partir d’un polynôme générateur primitif de degré k, détecte toutes les erreurs simples et doubles si la séquence d’entrée est de longueur au plus égale à 2k - 1.
7 - Tout générateur de clé construit à partir d’un polynôme générateur de la forme g(x)=(x Å 1).f(x) avec f(x) polynôme primitif de degré k, détecte toutes les erreurs impaires et doubles, donc en particulier les erreurs simples, doubles et triples, si la séquence d’entrée est de longueur au plus égale 2k - 1.
8 - Tout générateur de clé construit à partir d’un polynôme générateur de degré k, détecte tous les types d’erreurs de longueur inférieure ou égale à k dans un message de longueur n (n > k).
9 - Si le polynôme générateur choisi est irréductible de degré k, alors il détecte ces erreurs répétitives avec une probabilité proche de 1-2-k. S’il n’est pas irréductible, il ne détecte ce type d’erreurs qu’avec une probabilité de 1-2-k/b, où b est la plus forte puissance relative au polynôme décomposé en facteurs irréductibles.
Ces propriétés montrent que le polynôme générateur joue un rôle capital, selon son type (primitif, irréductible, quelconque) et selon son degré. Même avec un polynôme de degré réduit, on constate que la vérification de clé est dotée d’un pouvoir de détection de fautes élevé, quelles que soient les hypothèses de fautes supposées.
A chaque code détecteur d'erreur est associé une distance caractéristique "la distance minimale de HAMMING".
Un code de distance dmin détectera toute les configurations de dmin - 1 erreurs.
1.3.Réalisation d’un C.R.C.
Deux méthodes permettent de réaliser le C.R.C :
· La division polynomiale
· La méthode du OU-Exclusif
1.3.1.La division polynomiale
Une suite d’informations numériques représente un message. A tout message est associé une représentation algébrique, c’est-à-dire un polynôme de degré n-1 si le message comprend n informations.
Le message m = [ an-1 a n-2 an-3 ... a 2 a1 a0 ] est associé à un polynôme m(x) :
m(x) = an-1.Xn-1  an-2.Xn-2
an-2.Xn-2  ...
...  a1.X1
a1.X1  a0 ,
a0 ,
où X est une variable muette et les coefficients ai des valeurs binaires. Par convention, le coefficient an-1 est le premier bit transmis et correspond au plus fort degré du polynôme. Par exemple, le message n=(1,0,1,1,0,0,0,1) donne le polynôme n(x) = x7  x5
x5  x4
x4  1.
1.
L’opérateur  (OU Exclusif) est utilisé car nous ne considérons que des valeurs binaires, chaque bit du message étant traité séparément. L’algèbre sur les polynômes modulo 2 se définit par les opérations binaires suivantes : l’addition, la soustraction, la multiplication et la division. En arithmétique modulo 2, l’addition et la soustraction sont identiques.
(OU Exclusif) est utilisé car nous ne considérons que des valeurs binaires, chaque bit du message étant traité séparément. L’algèbre sur les polynômes modulo 2 se définit par les opérations binaires suivantes : l’addition, la soustraction, la multiplication et la division. En arithmétique modulo 2, l’addition et la soustraction sont identiques.
La division polynomiale est une division de m(x) par g(x) qui consiste à chercher un quotient q(x) et un reste r(x) de degré inférieur à celui de g(x) tel que :
m(x) = [q(x)  g(x)]
g(x)]  r(x)
r(x)
ou : m(x) - [q(x)  g(x)] = r(x)
g(x)] = r(x)
Cette deuxième forme fait apparaître un mécanisme de soustractions successives où g(x) est décalé de k rangs à gauche, c’est-à-dire multiplié par xk, afin d’atteindre le monôme de plus haut degré de m(x). Alors, q(x) possède un monôme en xk.
Une séquence d’informations correspondant au polynôme m(x) est comprimée au moyen d’une division de m(x) par un polynôme générateur g(x). La clé est le résultat de cette division : soit le quotient, soit le reste selon le type de réalisation effectué.
Posons le polynôme générateur g(x) = xk + bn-1.xn-1 + ... + b1.x1 + 1
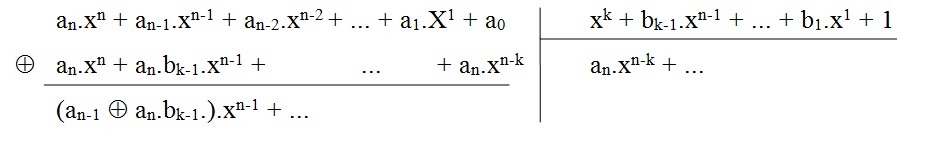
1.1.Réalisation pratique d’un C.R.C. par la méthode de la division polynomiale
Le principe de la division de deux polynômes peut être mis en oeuvre de façon :
- · matériel,
- · logiciel.
D’un point de vue matériel, des registres à décalage et des OU-exclusifs sont utilisés, et peuvent avoir une structure série ou parallèle. La clé est alors le reste de la division de m(x) par g(x) qui est le contenu final du registre à décalage
Pour la structure série, les données arrivent en série sur la ligne d’informations. Avec une structure parallèle, les données arrivent sur plusieurs lignes d’informations.
Les générateurs de clé série (voir Figure 8) et parallèle (voir Figure 9) construits à partir d’un même polynôme générateur primitif ont la même efficacité.
Dans la structure série présentée ci-dessous, les informations arrivent par l’entrée E, puis entrent dans le registre à décalage.
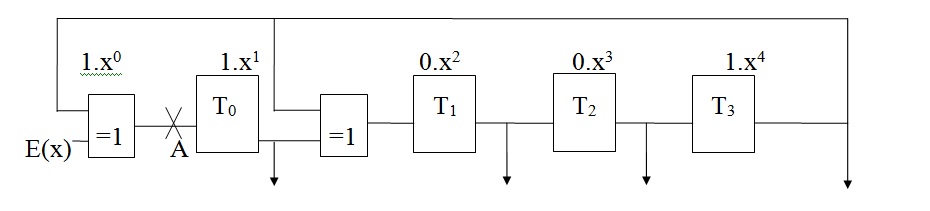
Figure : Générateur de clé de type SERIE avec g(x) = x4 + x + 1
Soit la séquence d’entrée (1,1,0,1,0,0,0,1,1), soit le polynôme d’entrée E(x) = x8+x7+x5+x+1.
Les états des registres sont décrits pour chaque front d’horloge dans le Tableau : Etats des registres d'un générateur de clé de type série.
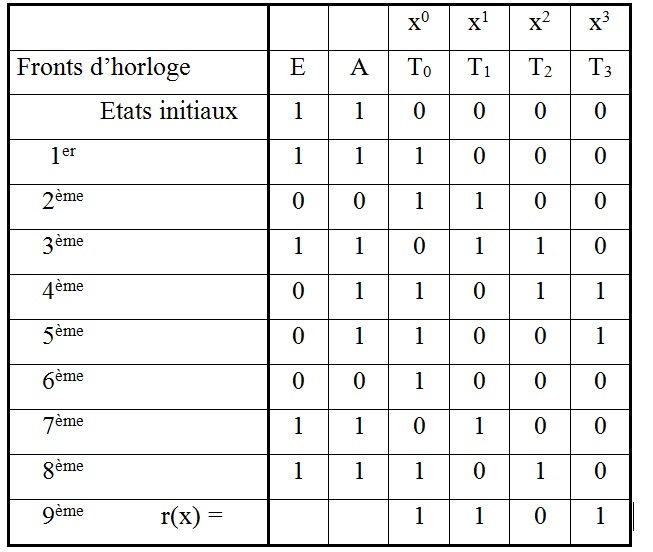
Tableau : Etats des registres d'un générateur de clé de type série
E(x) = [ q(x)  g(x) ]
g(x) ]  r(x)
r(x)
d’où E(x)/g(x) = q(x)  [ r(x)/g(x) ]
[ r(x)/g(x) ]
Le contenu final du registre est égal au reste de la division. De la même manière, nous pouvons construire un générateur à entrées parallèles.
Les informations en série notées (an-1, an-2, an-3, an-4, ..., a1, a0) sont groupées par bloc de 4, soient (an-1, an-2, an-3, an-4 / an-5, an-6, an-7, an-8 / ...) et présentées en parallèle sur chacune des entrées E0, E1,.E2, E3. En un seul front d’horloge, le résultat est établi pour ces 4 valeurs.
Soient y0, y1,.y2, y3, les états des registres à un instant « t » quelconque et a, b, c, d, les valeurs des registres évoluant suivant le Tableau : Etats des registres d'un générateur de type parallèle.
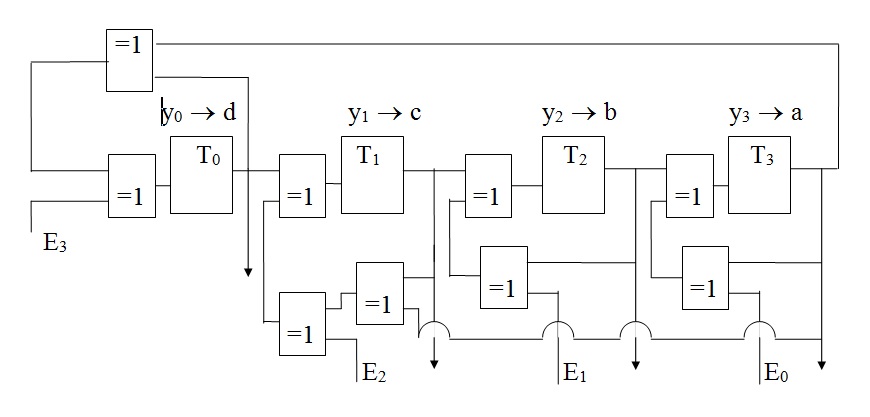
Figure : Générateur de clé à entrées parallèles avec g(x) = x4 + x + 1
La division polynomiale nécessite plus de cycles machine puisqu’il faut autant d’opérations (décalage + OU exclusif) que de bits contenus dans le message à contrôler.
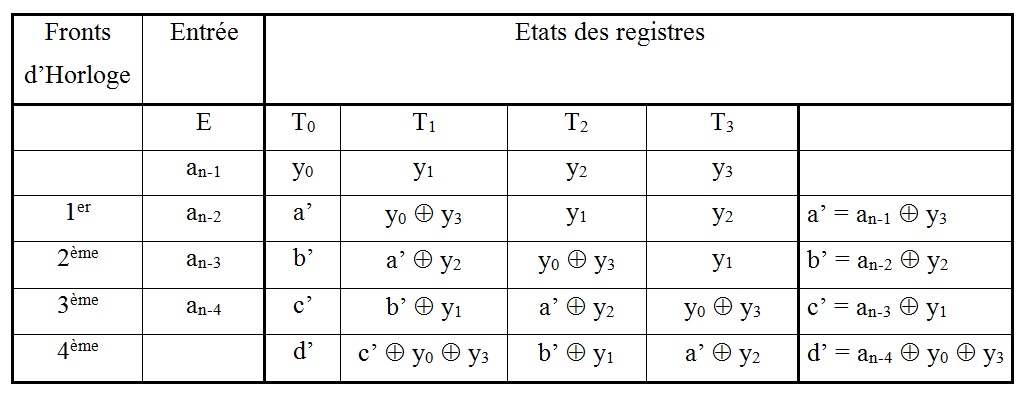
Tableau : Etats des registres d'un générateur de type parallèle
Nous obtenons les 4 fonctions suivantes :
a = a’  y2 = an-1
y2 = an-1  y3
y3  y2
y2
b = b’  y1 = an-2
y1 = an-2  y2
y2  y1
y1
c = c’  y0 = an-3
y0 = an-3  y3
y3  y1
y1  y0
y0
d = d’ = an-4  y0
y0  y3
y3
1.3.2.Méthode et réalisation pratique d’un CRC à partir d’un OU-Exclusif
Il existe une autre méthode afin de déterminer la clé. L’obtention d’une clé peut faire appel à un registre à décalage où certains bits sont bouclés sur l’entrée par l’intermédiaire de la fonction logique OU-Exclusif (Figure : Registre à décalage 16 bits (générateur de clé)). La clé correspond alors au contenu final du registre après passage en série de l’ensemble des informations. La longueur du registre ainsi que les bouclages sont fonction du polynôme P(x) qui, pour des applications usuelles, est généralement de degré 8 ou 16.
Soit P(x) = x16 + a15.x15 + a14.x14 + ... + a1.x + a0 avec a15 ... a0 = « 0 » ou « 1 »,
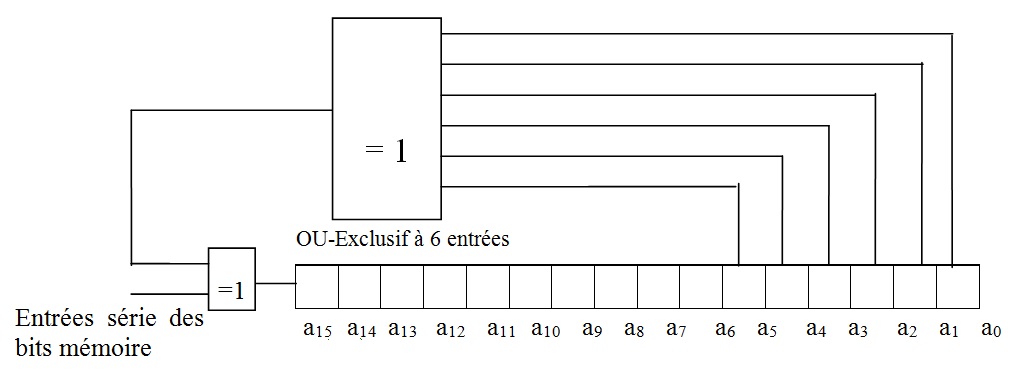
Figure : Registre à décalage 16 bits (générateur de clé)
La clé obtenue grâce à ce principe peut également être calculée par logiciel avec un algorithme adapté. L’algorithme correspondant s’obtient en observant le contenu du registre après 16 décalages successifs.
Si (y0 ... y15) est l’état initial du registre à t = 0 et (a0 ... a15) les 16 bits du message d’entrée, alors le contenu final du registre (x0 ... x15) après 16 décalages sera :
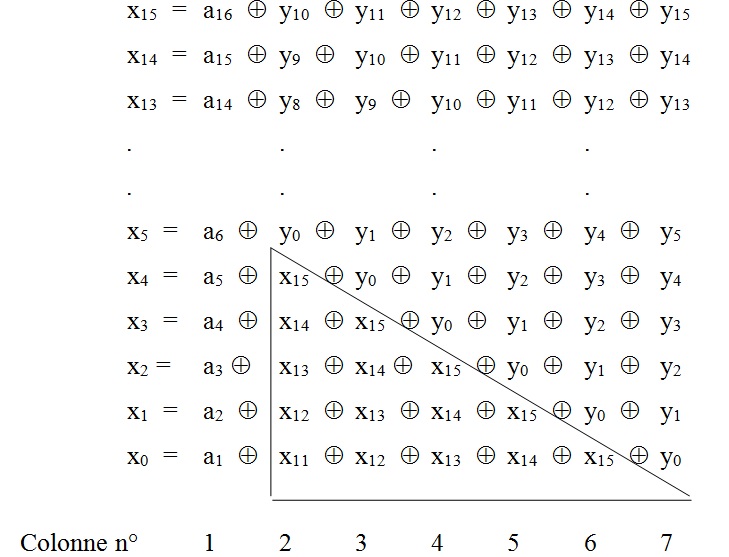
La colonne 1 représente la totalité du message d’entrée, les colonnes 2 à 7, hors la zone encadrée, représentent le contenu initial du registre décalé respectivement de 5 à 0 rangs.
Il ne reste plus alors qu’à effectuer les OU-Exclusifs entre les valeurs issues du bouclage (partie encadrée). Celles-ci seront déterminées par simple lecture à l’adresse pointée par l’adresse du début du tableau indexée de la valeur du quintuplet.
Ces valeurs seront lues directement dans un tableau de 25 = 32 éléments dans lequel on trouve, pour chaque quintuplet (x15, x14, x13, x12, x11), la valeur correspondante de x15, x15  x14, x15
x14, x15  x14
x14  x13 , x15
x13 , x15  x14
x14  x13
x13  x12, x15
x12, x15  x14
x14  x13
x13  x12
x12  x11.
x11.
1.4. Les codes correcteurs d’erreurs (codes de HAMMING).
Il est important de ne pas confondre distance de Hamming et codes de Hamming. Les codes de Hamming sont des codes détecteurs et correcteurs d’erreurs particuliers.
1.4.1.Principe des codes de Hamming
Si un transfert d’informations n’est pas correct, il existe 2 manières de retrouver la donnée :
· en demandant la ré-émission du message,
· en corrigeant l’erreur.
Il n’est pas toujours possible de demander une ré-émission du message. Le fait de corriger ces erreurs de transmission est alors primordial.
Les codes de Hamming permettent de détecter et de corriger les erreurs simples.
La méthode consiste à ajouter à un message de M digits, K digits de contrôle constituant ainsi un ensemble de (M + K) digits.
Il faut pour un mot de taille M digits, K digits de contrôle, or K digits ne permettent de définir que 2K combinaisons, d’où :
M + K + 1 £ 2K
Ce qui donne pour différente valeur de M, le tableau suivant :
|
M (bits) |
K (contrôle) |
|
4 |
3 |
|
8 |
4 |
|
16 |
5 |
|
32 |
6 |
1.4.2.Utilisation des Codes de Hamming
Pour montrer de quelle façon sont élaborés ces digits, on se place dans le cas d’un message de 4 digits (M = 4) ; 3 digits de contrôle (K = 3) sont alors nécessaires.
L’ensemble du message codé constitue alors un mot de 7 digits écrit sous la forme :
X = [ a1, a2, a3, a4, a5, a6, a7 ]
Les K digits de contrôle sont placés en a1, a2 et a4 sous réserve qu’il y en ait au moins un dans chacun des groupes (a1, a3, a5, a7), (a2, a3, a6, a7) et (a4, a5, a6, a7). Les digits de contrôle sont disposés de façon à ne contrôler que des digits « informatifs » et non d’autres digits de contrôle.
Les états des digits de contrôle sont donnés par les relations suivantes :
a1 = a3  a5
a5  a7
a7
a2 = a3  a6
a6  a7
a7
a4 = a5  a6
a6  a7
a7
Les codes de Hamming sont des codes détecteurs d’erreurs mais aussi correcteur d’erreurs. Il est donc possible de déterminer la position de l’erreur dans un message codé.
Dans notre exemple, l’erreur peut se placer parmi 7 positions. Il est alors nécessaire d’utiliser 3 bits pour coder en binaire la position de l’erreur dans le message codé.
La position de l’erreur se note en binaire [e3, e2, e1 ], et les états e3, e2 et e1 sont définis de la manière suivante : e1 = a1  a3
a3  a5
a5  a7
a7
e2 = a2  a3
a3  a6
a6  a7
a7
e3 = a4  a5
a5  a6
a6  a7
a7
A l’émission, les égalités e3 = e2 = e1 = 0 doivent être assurées, ce qui signifie qu’aucune erreur n’est détectée.
Si les égalités ne sont pas vérifiées, la position de l’erreur est indiquée dans le Tableau 3 : Position du bit erroné en fonction du code binaire de l’erreur ci-dessous :
|
Position de l’erreur |
e3 |
e2 |
e1 |
digit n° |
|
Aucune erreur |
0 |
0 |
0 |
|
|
a1 |
0 |
0 |
1 |
1 |
|
a2 |
0 |
1 |
0 |
2 |
|
a3 |
0 |
1 |
1 |
3 |
|
a4 |
1 |
0 |
0 |
4 |
|
a5 |
1 |
0 |
1 |
5 |
|
a6 |
1 |
1 |
0 |
6 |
|
a7 |
1 |
1 |
1 |
7 |
Tableau : Position du bit erroné en fonction du code binaire de l’erreur
X = [ a1, a2, a3, a4, a5, a6, a7 ] E = [e3, e2, e1 ]
Les codes de Hamming ne détectent pas l’erreur double. Pour y parvenir, un digit de contrôle supplémentaire (bit de parité) portant sur l’ensemble du message X est ajouté. La longueur du nouveau message codé est alors (M+K+1) digits. Après transmission du message, ce dernier est contrôlé afin de vérifier sa validité.
Si la parité globale est inexacte : le test précédent est appliqué au mot de (M+K) digits :
- · Si une erreur simple, double ou triple est détectée, elle est corrigée.
- · Si aucune erreur n’est détectée le mot est exact, l’erreur porte sur le dernier digit de contrôle global.
Si la parité globale est exacte, il y a 0 ou 2 erreurs ; le test de Hamming est appliqué.
- · Si aucune erreur n’est détectée, il n’y a pas d’erreur.
- · Si une erreur est détectée, il y a 2 erreurs, le mot est faux et aucune correction n’est possible.
English
